harris角点检测

发表于 |

简介

  • 角点检测是计算机视觉中获取图像特征的一种方法，在运动检测、图像匹配等任务中都有比较广泛的应用。
  • 角点被定义为两条边的交点，由于视觉任务的特殊性，角点检测的鲁棒性一般都是从平移、灰度变换、旋转、尺度变换等角度去评价。
  • 最早有Moravec角点检测算法，是通过计算自相关函数，找到局部方差和最大的点，作为角点，但是这种方法只能比较8个方向(8邻域)的特征变换，而且自相关函数的窗口是方形的，且是二元的，因此响应函数可能会有噪声。

harris角点检测讲解

像素点描述

  • 窗口发生$[u,v]$移动时，滑动窗口的像素灰度变换描述如下(借鉴了自相关函数的概念)

$$E(u,v) = \sum\limits_{(x,y) \in W(u,v)} {w(x,y){[I(x + u,y + v) - I(x,y)]}^2}$$

$[u,v]$是窗口的偏移量，$(x,y)$是窗口内的像素位置，$w(x,y)$是窗口函数，一般有常数窗口(1 inside and 0 outside)或者高斯窗口。

  • 因此在灰度变换平缓的区域，一般$E(u,v)$都比较小，而在灰度变换比较剧烈的区域，$E(u,v)$很大。

$E(u,v)$泰勒展开

  • 利用泰勒公式，将$I(x+u,y+v)$进行泰勒展开，得到下式

$$E(u,v) = \sum\limits_{(x,y) \in W(x,y)} { (u I_x + v I_y)^2} = \sum\limits_{(x,y) \in W(x,y)} {\left[ u \; v \right]
\left[ {\begin{array}{*20c}
{I_x^2}& I_x I_y\\
I_x I_y & {I_y^2}
\end{array}} \right]
\left[ u \; v \right]^T}$$

令$M = \sum w(x,y){\left[ \begin{array}{*20c}
{I_x^2}& I_x I_y\\
I_x I_y & {I_y^2}
\end{array} \right]} $，则有

$$E(u,v) = \left[ u \; v \right]
M
\left[ \begin{array}{*20c}
u\\
v
\end{array} \right]$$

M矩阵分析

  • 图像中主要有3种区域：flat area，line和corner，对于flat area，灰度在x和y方向上变化都比较平缓；对于line，灰度在一个方向上变化很剧烈(不一定是水平或者竖直方向，可以使任意方向)，在另一方向上变化平缓；对于corner，灰度在2个方向的变化都很剧烈。具体如下图所示

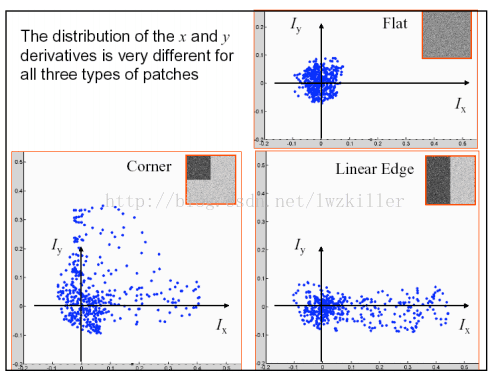
image

  • 特征值对应特征向量的权重，特征向量可以使任意方向的。对于M矩阵的特征值，如果2个特征值都很大，则可以认为是corner，如果只有1个大，则可以认为是line，如果2个都小，则可以认为flat area。

  • 因此定义变量$R$，度量角点响应，计算方法如下

$$R=det(M)-k(trace(M))^2$$

其中$det(M)=\lambda _1 \lambda _2$，$trace(M)=\lambda _1 + \lambda _2$。

其中$\lambda _i$是$M$的特征值，$k$一般取0.04~0.06左右，可以画出等高线如下，可以看出基本呈现出双曲线的形式，我们需要的是特征值都很大的点，因此这种度量方式符合要求。

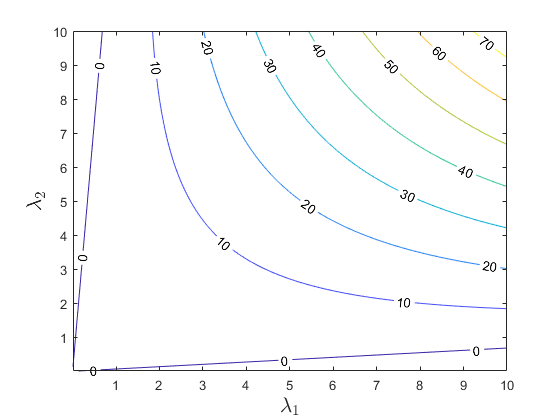
image

  • 绘图的matlab代码如下
clc,clear,close all
x = linspace(0.01, 10, 100);
[x, y] = meshgrid( x );

k = 0.06;

z = x.*y - k*(x+y).^2;
contour( x, y, z, 'ShowText','on' )
xlabel('$\lambda _ 1$', 'Interpreter', 'latex', 'FontSize', 16);
ylabel('$\lambda _ 2$', 'Interpreter', 'latex', 'FontSize', 16);

优缺点

  • 由上述表述可知，harris对于灰度仿射是具有不变性的（灰度值平移与尺度变换），对于图像旋转也是具有不变性的(计算只与特征值有关，与特征向量无关)，但是对于图像尺度变换不具有不变性(没有使用图像金字塔等结构)。

角点检测代码测试

  • 基于harris的角点检测算法代码如下，使用python+opencv完成，代码参考了opencv官网。

  • reference:https://docs.opencv.org/3.0-beta/doc/py_tutorials/py_feature2d/py_features_harris/py_features_harris.html

    import cv2
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

filename = 'image/chessboard.png'
img = cv2.imread(filename)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
img_after = img.copy()
gray = np.float32(gray)
dst = cv2.cornerHarris(gray, 2, 3, 0.04)

#result is dilated for marking the corners, not important
dst = cv2.dilate(dst, None)

# Threshold for an optimal value, it may vary depending on the image.
img_after[dst>0.01*dst.max()]=[255,0,0]

plt.figure( figsize=(12,6) )
plt.subplot( 121 )
plt.imshow( img )
plt.title("origianl")
plt.subplot( 122 )
plt.imshow( img_after )
plt.title("harris detection")
plt.show()
  • 检测效果如下所示
    image